Research Projects
Aeroacoustics
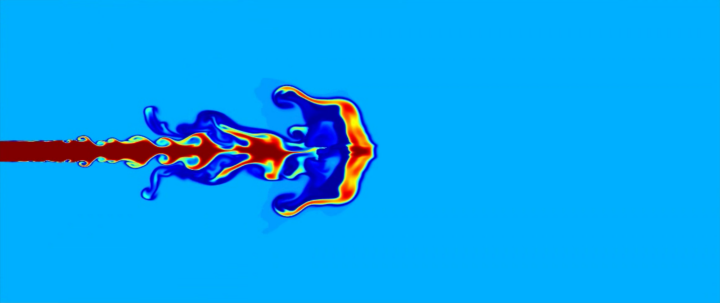
The main focus of the research field Aerocoacoustics is the direct numerical calculation of acoustics (DNC) in flows. The compressible equations of fluid mechanics are solved with the in-house code FLEXI. In contrast to common hybrid calculation approaches, the acoustic field is implicitly contained in the solution due to the compressible approach. This enables the prediction of aeroacoustic effects based on a coupling between hydrodynamics and acoustics. The challenge lies in the multi-scale character of the length and energy scales of hydrodynamics and acoustics. The efficient calculation requires high-order methods, such as the Discontinuous Galerkin Spectral Element Method (DGSEM) implemented in FLEXI.
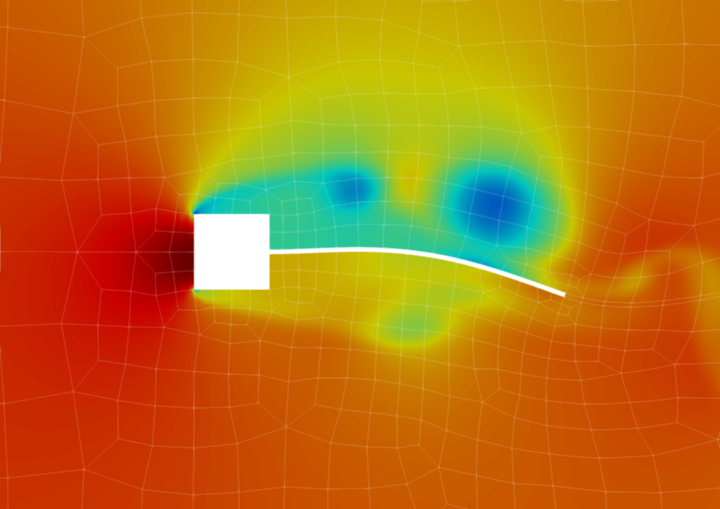
Examples of physical effects that are based on a coupling between hydrodynamics and acoustics are aeroacoustic feedback mechanisms. These can occur during the flow around wing profiles and vehicle mirrors as well as in flows over cavities in the form of Rossiter feedback. A common feature is the generation of total noise components, which cannot be predicted using classical hybrid simulation approaches due to the lack of the two-way coupling between hydrodynamics and acoustics.
Fluid-Structure-Interaction
Besides the efficient and highly accurate numerical simulation of fluids, coupled problems represent another field of work in the numerics research group. Due to increasing computational power, the solution of these kind of multiphysics problems is becoming possible in areas that are of industrial interest. Especially the interaction between fluids and structures plays a significant role in nature and engineering. Examples can be found e.g. in flow-induced oscillations of wings and buildings as well as in bio-engineering.
For this reason, there is a large demand for software to efficiently solve coupled problems. The numerics research group is active in different key areas of coupled simulations. These areas include methods to solve the equations of fluid dynamics on moving grids (e.g chimera methods or arbitrary Lagrangian-Eulerian formulations) and to alter a fluid grid based on the deformation of a immersed structure. Another feature are the coupling algorithms used both in space and time.
To this end, the DG fluid dynamics solver FLEXI is incorporated into a framework for the solution of coupled fluid-structure-interaction problems. Special emphasis is put on flexibility and the option to include different structural solvers. Possible areas of application include the simulation of flexible wind turbine blades, which are modeled as one-dimensional beams.
HOPR
Mesh generation
Numerical methods in computational fluid mechanics usually require a computational grid. While low-order schemes, such as first or second order Finite Volume methods require very fine meshes, for high order schemes such as DG very coarse meshes are sufficient. In order to obtain a sufficient approximation of geometry despite the coarse grid, so-called curved meshes are required. The working group at IAG concerned with mesh generation focuses on the development of methods generating curved meshes for DG methods. For this purpose the open-source grid generator HOPR was developed, which can generate unstructured, curved meshes and also supports non-conforming interfaces.
Generation of computational meshes optimized for DG
The elements of today's standard mesh generation tools have almost exclusively linear element edges. In industrial applications, the geometries that have to be meshed are very complex and usually have curved boundaries. In contrast to classical low-order methods in high-order methods, it is necessary, to also employ a high-order representation of the geometry in order to be able to guarantee a sufficiently accurate boundary representation on very coarse grids.
The discretization of the curved boundary surfaces is thus achieved by a high-order representation of the elements. The basic idea is that existing linear meshing software can still be used and that high-order elements can be generated from curved surface geometries with the help of additional data.
 |
 |
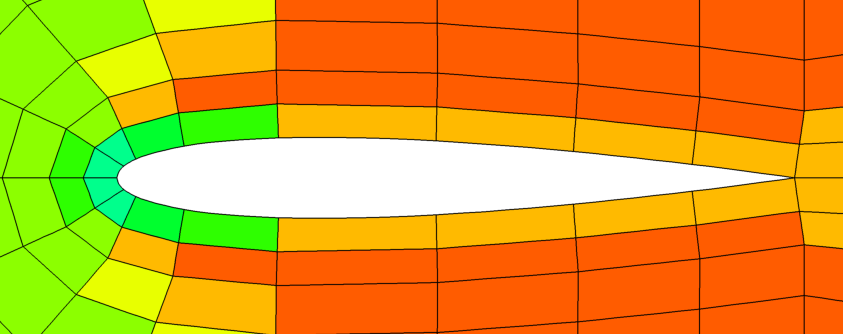
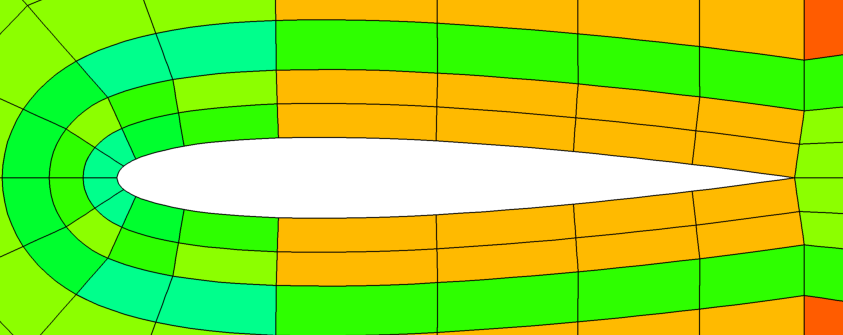 |
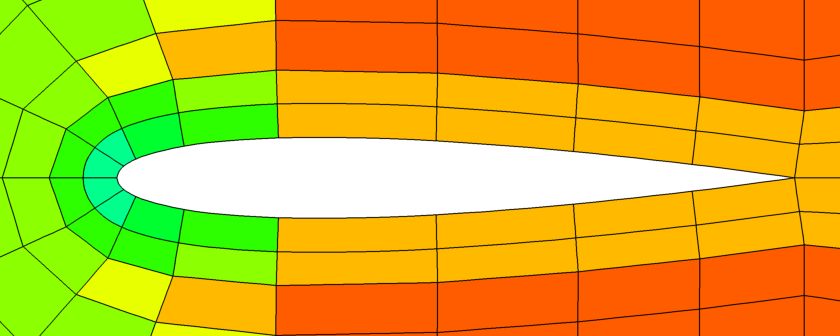
| Picture 1: Mesh Jacobian of a NACA0012 profile: linear mesh (left), first cell layer curved (center), fully curved (right) | ||
Concerning surface data, a distinction is made between two concepts, on the one hand a continuity-based approximation, which e.g. provides continuous transition between two grid cells by means of normal vectors, and an interpolation approach, which can better represent the surface by using additional points. The volume mapping of the elements can then be created e.g. by a linear combination of the curved element surfaces.
In the case of boundary layer meshes, the linear combination can lead to invalid element mappings. A valid grid can be generated by an additional grid deformation in the volume, which is, however, very complex.
Since the research focus of the numerics group is in the area of DG methods, different implementation techniques of curved grids within DG methods are also investigated. Especially the use of curved non-conforming meshes is non-trivial: on one hand the meshes need to be watertight, i.e. the sides of adjacent curved elements of different sizes have to provide an identical geometry representation, on the other hand the polynomial resolution in the solver has to be high enough to ensure free-stream preservation on such meshes.
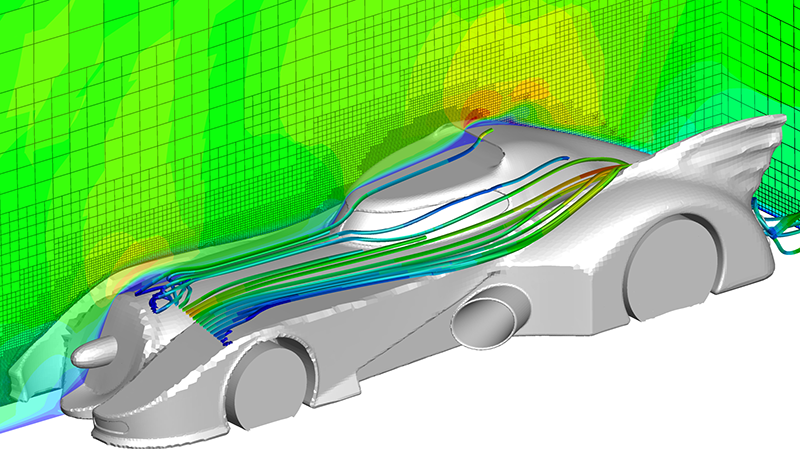
Picture 2: Unstructured, non-conforming mesh of a vehicle
HOPR
The mesh generator HOPR developed in the numerics group is an open-source toolkit for the generation of three-dimensional unstructured high-order meshes. These meshes are used in high-order methods such as Discontinuous Galerkin, Flux Reconstruction or Spectral Element methods.
 |
HOPR uses linear meshes as a basis for the generation of curved meshes, which can be generated by many common grid generators. These are enriched with high-order surface data to generate meshes that are curved either only at the boundaries or in the entire volume. There are several different techniques to choose from:
- Reconstruction using normal vectors
- Agglomeration of block-structured grids
- Import of supersampled surface data
For the generation of curved boundary layer meshes it is often necessary to propagete the strong deformation of the cells at the boundary further into the volume, which can be done for example by the means of different blending functions, radial basis functions or by solving an elliptical PDE for the displacement.
HOPR supports unstructured, hybrid grids composed of tetrahedra, pyramids, prisms and hexahedra. The program also integrates functions to prepare the domain decomposition in the solver by sorting the elements along space-filling curves. Since these curves are geometrically very compact, it is sufficient to divide these 1D curves into contiguous segments in the solver. This is a particularly simple and flexible domain decomposition approach, which works well for Cartesian and unstructured meshes.
The development of HOPR is performed by Numerics Research Group.
Scale-resolving Simulations of Turbulent Flows using High-Order Methods
The group of Prof. Munz is involved in the development of high-order numerical methods and models for scale-resolving simulation of turbulent flows (large eddy simulation, LES). Due to the strong interactions between the numerical discretization and the modeling terms occurring in these kind of simulations, a highly accurate and robust high-order methods has significant advantages as a baseline scheme for LES compared to low-order methods. Beside research in the development and increasing efficiency of LES, the numerics group also investigates different kinds of closure methods for free and wall-bounded flows. Among other topics, basis enrichment using physically motivated wall function, optimal high-order filtering procedures and data-driven closure models are being developed.
Multi-Phase Flow
The research group works on the development of sharp- as well as diffuse interface methods for the simulation of multi-phase flow simulation under extreme ambient conditions (near the critical point of the involved materials). The processes in these flow regimes pose significant challenges to the numerical methods. The compressibility of the involved fluids has a major influence on the flow behavior and furthermore highly accurate equations of state are required to account for the complex material behavior. The use of implicit-explicit splitting techniques allows the simulation of more complex problems, due to the significant increase in computational efficiency.
PICLas – Plasma Simulations
Rarefied plasma flows are efficiently modeled by kinetic particle methods by combining the Particle-In-Cell (PIC) method with the Direct Simulation Monte Carlo (DSMC) scheme. The PIC module is an Eulerian-Lagrangian scheme which approximates the self-consistent evolution of charged particles and electromagnetic forces. The simulated particles move freely through the computational domain whereas the electromagnetic fields are computed by a grid-based DGSEM. Both layers of the PIC method are coupled via deposition and interpolation routines, which map physical quantities from the grid-based solver to the particles and vice-versa. The DSMC module is a pure particle approach which approximates momentum and energy transfer as well as chemical reactions. Within the PIC and DSMC solver, the computational load is reduced by combining several real particle within a simulated particle.
High-Order Particle-in-Cell Methods
The development of numerical methods is currently focused on the handling of unstructured, curvilinear meshes and the required particle-mesh coupling. Another focus is the development of high-order time-integration methods for the full PIC method. The area of application of the PICLas framework includes microwave oscillators like gyrotrons or gyro-traveling wave tubes, laser-plasma interactions or space applications.
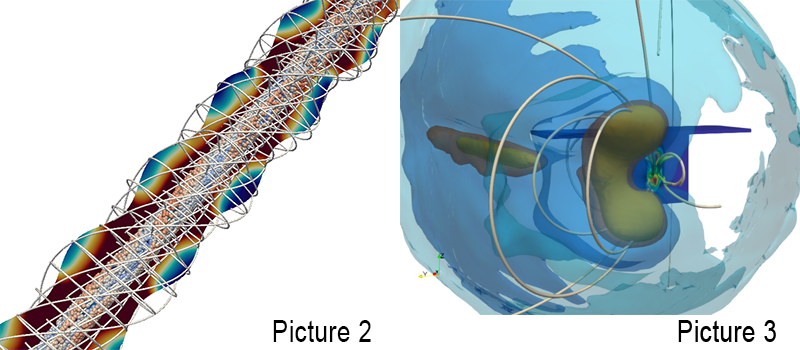
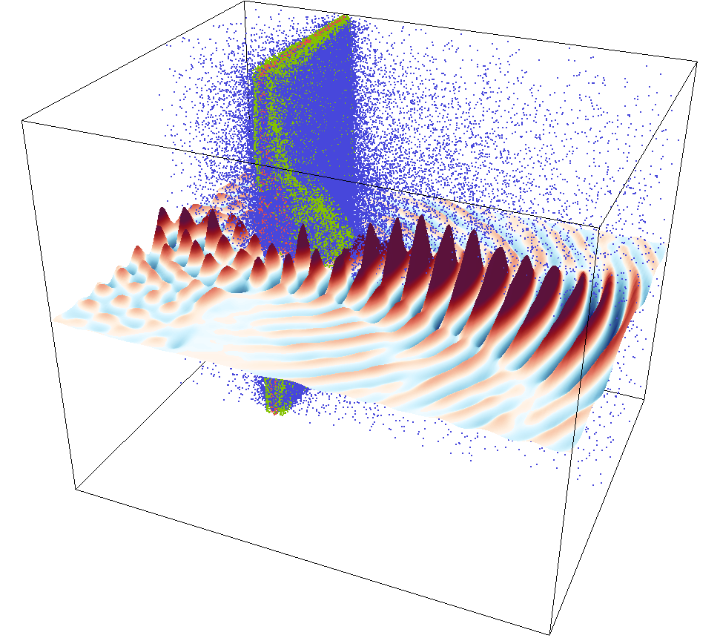
Picture 1:
Simulation of a gyro-twt. The curved grid lines as well as the instantaneous magnetic field and particle distribution are shown.
Picture 2:
Profiles of the electron density around a satellite shielded by a magnetic field.
Coupled PIC-DSMC Simulations of laser-driven ablative Expansion
Laser-driven ablative processes are encountered within solid-state physics or material processing. The currently used computer models for the laser-solid interaction are based on the molecular dynamic simulations. These methods are restricted to the interaction of the laser pulse with the solid-state and processes occurring within the solid phase. The expansion of the produced plasma and the impact on further processes is not considered within these simulations. However, this expansion has to be modeled in order to predict the influence of the plasma on secondary laser pulses or contamination processes.
The PIC-DSMC simulations continue the ablation process by analysing the plasma expansion process up to the mesoscale. Further analysis is focused on the question of weakening secondary laser pulses by considering the laser-plasma interaction. Thereby, the laser pulse is modeled as electromagnetic fields within the DGSEM solver. The predicted laser energy, which reaches the solid, is extracted from the PIC-DSMC simulation and forwarded to the molecular dynamic simulations as input parameters.
Contact: Jakob Dürrwächter und Thomas Kuhn
Uncertainty Quantification
The focus of this research field is the investigation and quantification of uncertainties in the context of flow simulations. The aim is to investigate the effects of uncertain input variables on the solution of the flow field. Possible uncertain input variables can be categorized into model uncertainties, geometry uncertainties and uncertain flow parameters.
The underlying idea is based on an extension of the flow equations by any number of stochastic dimensions. The mathematical concepts used and investigated range from classical Monte Carlo sampling methods to various polynomial chaos methods.
Current applications are uncertainties in the context of aeroacoustic flow simulations. The main research topic is noise generation at cavities whose physical mechanisms are highly sensitive to.
Prof. Dr.-Ing. Andrea Beck, M.Sc.

Andrea Beck
Prof. Dr.-Ing.Managing Director / Head of Numerical Methods in Fluid Mechanics